Combinatorics for Kittens

Example 2 - The Birthday problem

Ok. You've probably heard of this one, but let's take it from the top.

There are 365 days in the year. So how come, even in a smallish group, there's always a couple of people who share a birthday?

Freaky psychic powers, say some. Similar souls seeking each other out.

Let's look at it this way.

Consider a pile of cats. And three hundred and sixty five boxes. These are big boxes though - each one ould hold many cats.

And cats do like to play in boxes. How many ways can they play?
Cat 1 can choose any of the 365 boxes. Cat 2 can choose any of the 365 boxes. And so on.
So there are ways to arrange those cats.

But some of them - there are multiple cats in a single box. We don't think that's likely. So let's count how many ways we can arrange them WITHOUT overlap. Well, that's easy - from the previous page we know it's 365Cn - 365 boxes and fill up n of them. Obviously if we've more than 365 cats, it's zero. Note that it's nCm and not nPm because we don't care WHO shares a birthday in the group.

So there are ways of arranging them, and 365Cn 'good' ways, that is ways that do not share a birthday, of arranging them.

So what are the chances of getting a 'good' arrangement?

At this point you either get a calculator with a reallllly wide screen, or cheat a bit. You can do some cancellations, or use Stirlings approximation. (Which says that )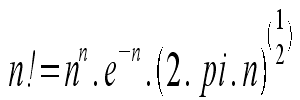

And an interesting thing happens when you graph it:

Around about 23-25 it becomes more likely that you DO have more than one kitten in a box (or person sharing a birthday) than you don't.